Hacking in Wine involves reverse engineering of Windows components and algorithms, and the rule is that we have to do it without looking at the Windows code, or disassembly. Instead, we write tests, checking the outputs and side effects of function call sequences, and then write code that would do the same thing.

It is a bit tedious and a long process, but most of the time it isn’t actually very hard… maybe not even very fun either. Most of the time, it doesn’t really deserve writing a story about it. Sometimes, it gets hard… and fun.

In this article I’m going to embed images and code snippets, they are only meant as illustrations, and are not directly usable. I’ve tried to keep them close to some actual code that you will be able to find there. Each image also have a corresponding Python source that was used to generate it.

Table of Contents

Transcendance

There’s a set of maths functions, called transcendental functions, which transcend algebra. They cannot be expressed as a finite sequence of algebraic operations⁽¹⁾, and cannot be exactly computed. Instead, what a computer can only achieve, is an approximated result. Of course, it is always possible to run a longer sequence of operations to achieve more precision in the result, but it will never be exact.

This includes a lot of very useful functions, such as trigonometric, exponential, or logarithm, which are used almost everywhere in games. They often end up being used to compute some aspect of the game state, which, in multiplayer games, may be compared against other players expected state.

Any difference in the states could mean there’s something weird going on, that some network packets got lost or that someone’s cheating. The games often then bail out and end the game session: It’s what happens in Age of Empires or Mortal Kombat 11, causing spurious disconnects when you try to start a multiplayer game in Proton.

Why are there any differences between the expected state and the other players’? Because each player may be running the game with a different C runtime, some are on Windows, some are now using Proton, and Wine. Maybe some could be playing on a console.

As these functions can only be approximated, and as finding a good approximation function is a complex task, almost every programming language provides an implementation of them. The C language runtime makes no exception here, and the C language standard even mandates it. The GNU glibc library, musl libc, and Windows msvcrt.dll or ucrtbase.dll, all provide them.

What the C language standard doesn’t mandate though, is how they must be approximated, and we’ll see, there’s an infinite number of ways to do so, all equally valid. And even if precision is nice to have, it is also sometimes costly to get, so trade-offs can be made between performance and precision.

Overall, and most of the time, the results returned from the evaluation of a certain transcendental function have very little chance to match the ones from another implementation. It could even happen with the same runtime, if it decides to use a different code path after some CPU feature has been detected (think SSE, FMA instructions etc…).

In our case, comparing almost any of the Wine maths functions with Windows ucrtbase.dll maths functions will show differences. Not so much, but enough to make games unhappy when a player uses Wine and another uses Windows.

⁽¹⁾ addition, multiplication, and raising to a power, or the inverse operation, subtraction, division, and root extraction.

Approximation

Function approximation is a large topic, so I will only focus on the most common approach for the functions we’re interested in, and I will use arcsine function as an illustration, because it has some properties that makes it easier.

The arcsine function looks like this:

Range reduction

The first step is about handling corner cases. This is straightforward, the arcsine function is only defined over the [-1; 1] interval, so anything outside of this range should return an error:

• if (x < -1 || x > 1) return math_error();

Then, we reduce the problem space to reduce the range of values where we want to actually compute an approximation. This is most often achieved by exploiting mathematical relations between functions.

For instance, with arcsine, you have the following properties:

• arcsine(-x) == -arcsine(x)

• arcsine(x) == pi / 2 - 2 * arcsine(sqrt((1 - x) / 2))

Which we can exploit to reduce the range of x values where we need to approximate arcsine to [0; 0.5]:

• if (x < 0) return -asinf(-x);

• if (x > 0.5) { float z = sqrtf((1 - x) / 2); return pi / 2 - 2 * asinf(z); }

Of course, this is only one possible reduction. There’s many other properties that can be exploited. For instance you also have:

• arcsine(x) == pi / 2 - arccos(x)

• arcsine(x) == arctan(x / sqrt(1 - x²))

• arcsine(x) == arccos(sqrt(1 - x²)), with x > 0

• etc…

If for some reason you found a better approximation of arccos, or arctan and you want to compute arcsine from it, it’s very much possible.

Of course, we’re not even limited to mathematical properties, and we can very well decide to split the value ranges into pieces, and find an approximation for each of these sub-ranges.

After the range has been reduced or split enough, we will now focus on computing the approximation. There’s plenty of ways, we could hardcode value in static tables, if we don’t care about the size in memory. Most of the time nowadays, polynomial approximation is used instead.

Polynomials

The idea is that for a continuous function f(x), x ∈ R and given a maximum error ε, you can always find:

• P(x) = p₀ + p₁x + p₂x² + ... + pₙxⁿ

So that ∀ x ∈ R, |f(x) - P(x)| <= ε. The smaller the maximum error, the higher degree P(x) will need to be.

Of course, there are an infinite number of such polynomials that can work, and plenty of ways to find one. For instance Taylor expansion is the most well known method, but some other classes of polynomials such as Chebyshev series are also sometimes used.

The Taylor expansion series of arcsine is actually very simple, and it can be expressed in the form of:

• arcsine(x) = x + x * P(x²)

We’ll use that for an additional range reduction, and compute the approximation of (arcsine(x) - x) / x using P(x²) instead:

An inconvenience with simple polynomials is that they tend to diverge quickly around their definition range bounds, and for a small ε value we may need to use a very large polynomial degree n.

The higher n is, the more computation we’ll have to actually do, and the errors will also not be spread evenly across the value range.

For instance, using the Taylor series as the polynomial expression, and for instance with a degree 2, we get the polynomial P(x) = 1/6·x + 3/40·x², and plotting it with arcsine, we can see it’s already pretty close:

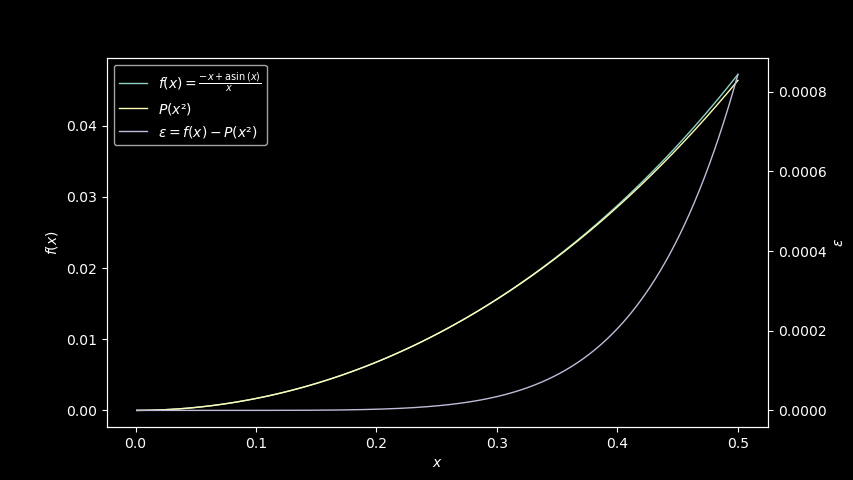
Good enough, right? Well, not very good if you look at the theoretical error. We could improve that by using the Taylor series expansion evaluated around 0.125, instead of 0.

We now get a P(x) = 0.00011432060688831153 + 0.16400250467599248·x + 0.09510025970319425·x² polynomial instead, with an improved error profile:

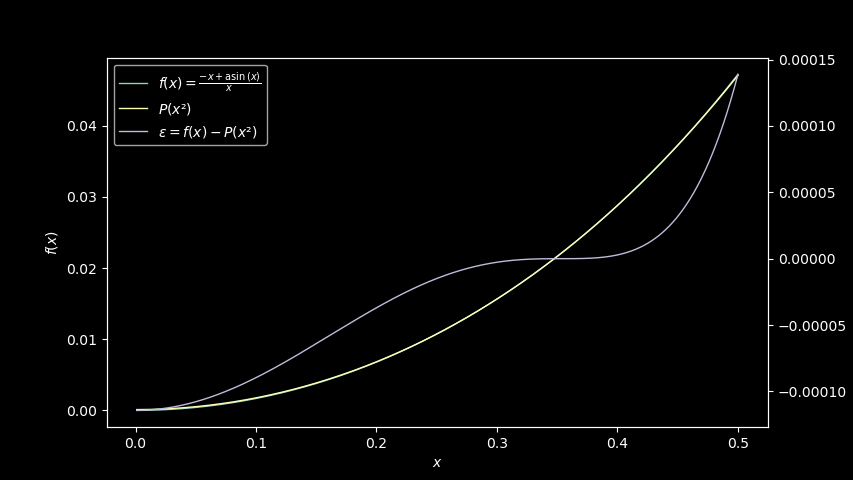
It’s better, and the error is more consistent over the range, but there’s a better way: Instead of a simple polynomial, we can use a rational polynomial of the form P(X) / Q(X), with:

• P(x) = p₀ + p₁x + p₂x² + ... + pₙxⁿ

• Q(x) = q₀ + q₁x + q₂x² + ... + qₘxᵐ

Rational polynomial are strange beasts, they cannot be expressed as simple polynomials but they share the same properties for function approximation. Although they also tend to diverge near the limits, they can have a better average error overall, for lower degrees n and m.

There too, several methods to compute them are available. One is the Padé approximant, or other algorithms such as Remez algorithm or minimax rational approximation also exist.

Note that all the functions are usually continuous on the value range and easily derivable, so we could very well use more brute force methods such as least squares method, or any other optimization algorithm too.

For arcsine, we can use polyrat to compute first degree polynomials P(x) = -5.233528614964622e-06 - 0.1764267746171257·x and Q(x) = -1.0610258247966033 + 0.5041027241138349·x, and immediately get 10 times better approximation than our best Taylor expansion:

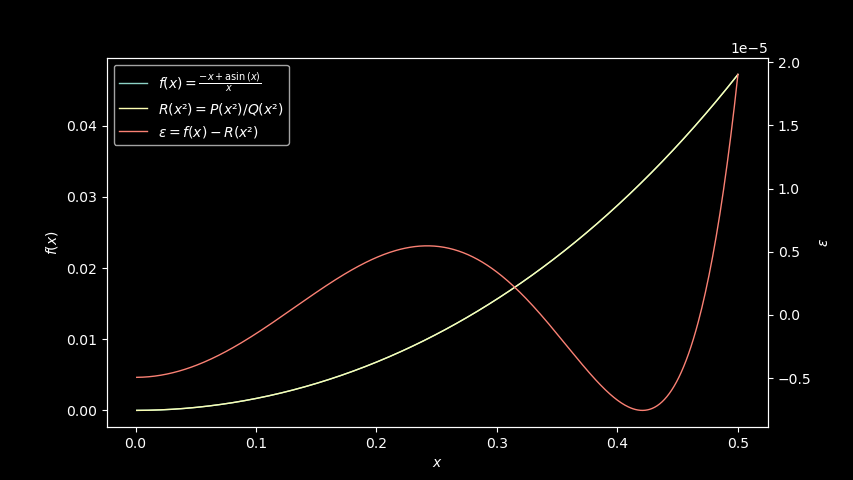
As you see, our maximum error is already around ε = 1e-5 with single degree polynomials. Using rational polynomials degrees 3 or 4, we can easily achieve something like ε = 1e-12 or better. It’s really just a matter of adding more computations.

The implementation we currently use in Wine uses a 4th degree P(x) and a first degree Q(x).

Computation

So, after we’ve found good polynomials, it will all be about evaluating them. We can do it the naïve way, in the same way they are expressed above, and compute P(x) = p₀ + p₁x + p₂x² + ... + pₙxⁿ and Q(x) = q₀ + q₁x + q₂x² + ... + qₘxᵐ, but we would need to compute x powers many times, and that may not be the most efficient.

Instead, polynomials can be expressed in multiple forms, some being more efficient for computing than others. The one that’s used by many C language implementations is the Horner form, where we factor x for each increasing power:

• P(x) = p₀ + x·(p₁ + x·(p₂ + ... + x·pₙ)...)

There exist other canonical forms, like the continued fraction for rational polynomial, but I don’t know if it can be used efficiently.

Computing the Horner form is easy, we start with the highest degree coefficient, compute x·pₙ, add the next coefficient, multiply by x, add the next, etc…

It is especially efficient on modern hardware because they have specialized CPU instructions called FMA for fused multiply-add, which perform a multiplication and an addition at the same time.

So, we now know how to approximate our arcsine function, we can even do it with an arbitrary high precision, by increasing our polynomial degrees. In theory, that would mean that we can get as good results as the Windows arcsine implementation? Well, no.

Computation is where things start to get tricky, and where the theory falls apart: computer can’t count, they make mistakes… all the time…

Floating-point

Computers can’t count. They can’t even represent most real numbers. Not exactly at least.

You don’t believe so? Run python -c 'print(1/10 + 2/10 - 3/10)' and see for yourself. Any child knowing about fraction and addition can tell you the answer is 0. But Python cannot, and it prints 5.551115123125783e-17 instead.

It’s not a language issue, every programming language will struggle at this unless it does some kind of rational computation.

What happens here is that computers are limited. They cannot represent arbitrary numbers efficiently and they need to work with a certain set of numbers, all based on powers of two. This is also the case for real numbers, using negative powers of two to represent decimal numbers. Any number which is not a power of two needs to be rounded to the best matching one.

They are also size limited, and they are only able to keep track of a similarly limited amount of information, either the information about the number digits, or about the power of two. Any number which requires either a larger, or smaller power of two, or which has too many digits to be represented will be truncated.

Then, even if two numbers can be represented exactly, the result of an operation on these numbers might not be, and will have to be rounded or truncated too.

There’s a standard which defines these representations and limitations, called IEEE 754 floating-point. It defines the format used to represent the numbers in memory, as well as how these rounding and truncations should be done, and how operations on other floating-point numbers need to operate.

(By Vectorization: Stannered, CC BY-SA 3.0)

Every addition, or multiplication, that operates on floating point number will follow that standard. And everything is done to prevent these rounding and truncations from causing invalid results, but 1ULP⁽²⁾ errors are common and usually considered harmless, especially when it comes to transcendental maths approximations.

⁽²⁾ Unit in the Last Place, the last bit in the IEEE floating-point representation

Moreover, these are rounding errors and they are thus heavily dependent on the values as well as on the order of the computed operations. So, the polynomials degrees, their coefficients, and the form used to compute them, all matter very much.

In the end, even with a very accurate theoretical approximation, if the operations we’re doing aren’t rounded in the same way as how Windows does it, there’s little chance we end up with the exact same value for every possible floating point value.

So yes, it looks bad, can we do something about it?

Solution

There’s actually only one good solution to this issue: games, or game engines, should implement and embed their own maths approximations.

And now, you know how to build your own, it’s not so hard and there’s even existing open-licensed reference implementations for some extra easy.

Including the implementation within the game will ensure that - assuming the hardware works the same, but most of the time it does - it would not depend on the runtime anymore. Whether you run on Windows or Wine, it will give you the exact same results.

Then, from Wine hacking perspective, it’s simply not fun. What if we could do better?

Fun?

What if we could find clues about the sequence of operations that were done by looking at the input and the results, taking into account the error that it produces?

It really sounds like looking into the cosmic background noise to figure what happens in the room next to you, but could that work?

Writing tests

First of all, we will want every comparison we do to be exact. We need all the bits of the compared values to match. So in order to avoid any trouble with floating-point and implicit rounding, we’re going to use a programming trick to access both the floating-point value and its representation, when we need to manipulate or compare it, as a 32bit integer value:

union float_value
{
    INT i;
    UINT u;
    float f;
};

As we have 32bit of information, it means that there is around 4 billion possible values. In addition, IEEE 754 defines 4 rounding modes that can be enabled globally, and which will apply to every floating-point operation that is done, possibly changing every result.

There’s Round to nearest, Round toward 0, Round toward +∞, and Round toward -∞. We want Wine implementation to match Windows implementation for all the values, regardless of the rounding mode in use, but for now we’ll just assume the default Round to nearest is used.

So, lets start by getting the easy cases out of the way. This includes all the special floating-point values IEEE 754 defines, as well as corner cases such as very small or out of range values.

NaN numbers: these are not valid numbers. They are in the following ranges:

• [0x7f800001; 0x7fc00000): Signaling NaNs

• [0x7fc00000; 0x80000000): Quiet NaNs

• [0xff800001; 0xffc00000): Signaling NaNs

• [0xffc00000; 0x00000000): Quiet NaNs

For all these, calling arcsine should return a Quiet NaN value:

static void test_asinf_nan( UINT min, UINT max )
{
    union float_value v, r;
    for (v.u = min; v.u != max; v.u++)
    {
        r.f = asinf( v.f );
        ok( r.u == (v.u | 0x400000), "asinf %#08x returned %#08x\n", v.u, r.u );
    }
}

Domain errors: these are invalid values for the arcsine functions, they are in the following ranges:

• [0x3f800001; 0x7f800001): (1.f; +inf]

• [0xbf800001; 0xff800001): (-1.f; -inf]

For all these, calling arcsine should return a Quiet NaN and set an error (not tested):

static void test_asinf_edom( UINT min, UINT max )
{
    union float_value v, r;
    for (v.u = min; v.u != max; v.u++)
    {
        r.f = asinf( v.f );
        ok( r.u == 0xffc00000, "asinf %#08x returned %#08x\n", v.u, r.u );
    }
}

Tiny values: these are valid values but very small, and arcsine should return the same value as input:

• [0x00000000; 0x38800000): [+0; +6.10352e-05)

• [0x80000000; 0xb8800000): [-0; -6.10352e-05)

The returned value should be the same as the input because the result is truncated. This is interesting to test because it is effectively a range reduction.

static void test_asinf_tiny( UINT min, UINT max )
{
    union float_value v, r;
    for (v.u = min; v.u != max; v.u++)
    {
        r.f = asinf( v.f );
        ok( r.u == v.u, "asinf %#08x returned %#08x\n", v.u, r.u );
    }
}

Lastly, two more easy values can be tested: 0x3f800000 (+1) and 0xbf800000 (-1):

Tests actually show that Wine is wrong here: our approximation may return truncated results, especially with non-default rounding modes, where Windows always returns ±π/2. Easy to fix and two less values to worry about.

static void test_asinf_pio2( UINT min, UINT max )
{
    union float_value v, r;
    for (v.u = min; v.u != max; v.u++)
    {
        r.f = asinf( v.f );
        ok( r.u == ((r.u & 0x80000000) | 0x3fc90fdb) /* ±π/2 */, "asinf %#08x returned %#08x\n", v.u, r.u );
    }
}

Now only the [0x38800000; 0x3f800000) and [0xb8800000; 0xbf800000) ranges remain, we can add a few more tests to validate that we can indeed use the asin(-x) = -asin(x) range reduction we talked about previously:

static void test_asinf_sign( UINT min, UINT max )
{
    union float_value v, o, r;
    for (v.u = o.u = min; v.u != max; v.u++, o.u = v.u)
    {
        r.f = asinf( v.f );
        o.u ^= 0x80000000;
        o.f = asinf( o.f );
        o.u ^= 0x80000000;
        ok( r.u == o.u, "asinf %#08x returned %#08x\n", v.u, r.u );
    }
}

00d4:math: -503316375 tests executed (0 marked as todo, 0 failures), 0 skipped.

These tests results look… alright? Good, so now it’s reduced down to the [0x38800000; 0x3f800000) range. Only about 112 million values to match.

Checking errors

We could try plotting Wine arcsine and Windows arcsine and see if we can spot any pattern, but it’s actually pretty pointless: they are very close to each other, they only mismatch for a few hundred thousand values, and when they do, the mismatch is only about the last bit of the value, not something that you will see.

Instead, we need to figure how much is 1ULP error, for every x. Note that it’s not 1ULP relative to x, but relative to arcsine. We keep these ULP stored as 64bit floats, because they are too tiny otherwise:

class Float:
  def from_repr(data):
    import struct
    reprs = struct.pack(f'{len(data)}i', *data)
    float = struct.unpack(f'{len(data)}f', reprs)
    return np.array(float, dtype=np.float32)

  def repr(data):
    import struct
    float = struct.pack(f'{len(data)}f', *data)
    reprs = struct.unpack(f'{len(data)}i', float)
    return np.array(reprs, dtype=np.int32)

  def ulp(data):
    min_data = Float.from_repr(Float.repr(data) & 0x7f800000)
    ulp_data = Float.from_repr(Float.repr(min_data) + 1)
    return np.float64(ulp_data) - np.float64(min_data)

asin_ulp = utils.Float.ulp(np.arcsin(x))

Then we load the 32bit values, and compute the differences using 64bit floating-point which should be able to represent tiny values:

x = utils.Float.from_repr(range(xmin, xmax))
wine_asinf = np.fromfile(open(f'{dir}/asinf-{xmin:08x}-{xmax:08x}-wine.dat', 'rb'), dtype=np.float32)
msvc_asinf = np.fromfile(open(f'{dir}/asinf-{xmin:08x}-{xmax:08x}-msvc.dat', 'rb'), dtype=np.float32)

diff = np.float64(wine_asinf) - np.float64(msvc_asinf)

We can now check that there’s indeed only a few differences, and ignore values where the results match already:

assert len(x[diff != 0]) <= 320000

An we plot the differences, relative to the ULP:

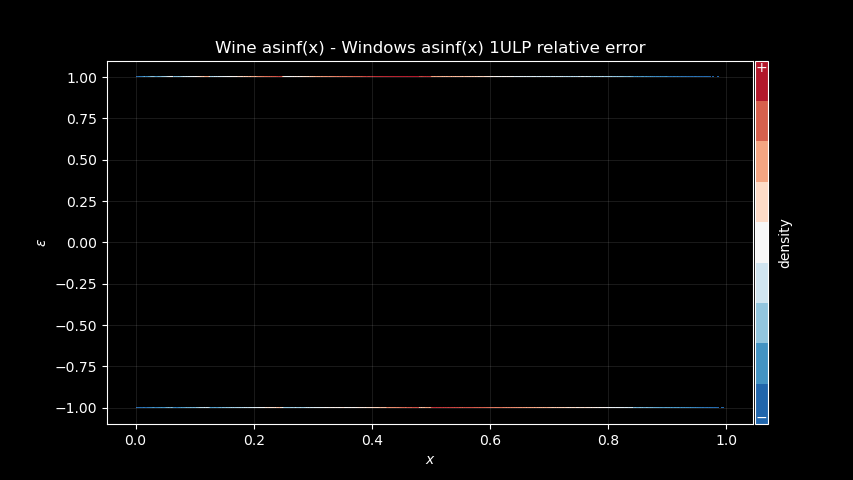
As you can see, differences are really all ≤ ±1ULP. The color also corresponds to the density of points, blue is the least dense, red the most dense⁽³⁾. And as you can see, the density is not uniform, which means that Wine implementation is definitely biased toward some direction.

⁽³⁾ note that the scale is not linear, and instead the colors bands are equalized for improved visibility.

In any case comparing these doesn’t give us much information, so let’s try something else. For instance, let’s compare Wine and Windows implementation to a higher precision arcsine, and let’s see if we can get something useful out of the error profile:

wine_diff = np.float64(wine_asinf) - np.arcsine(np.float64(x))
msvc_diff = np.float64(msvc_asinf) - np.arcsine(np.float64(x))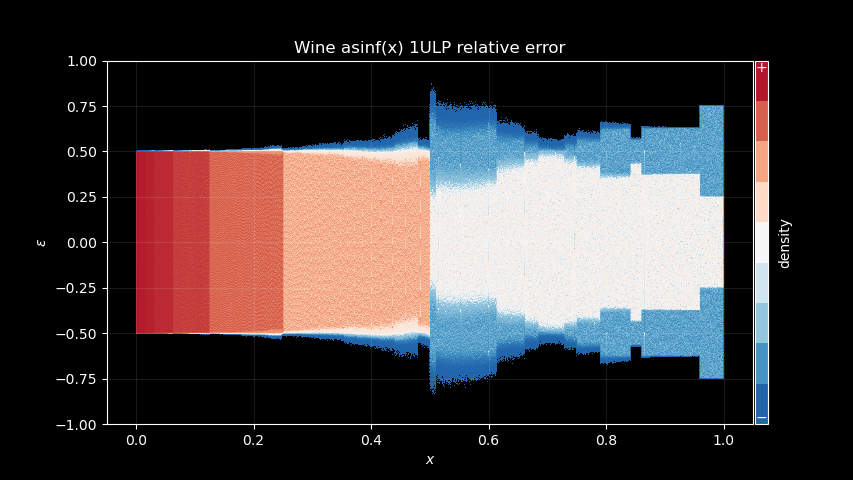

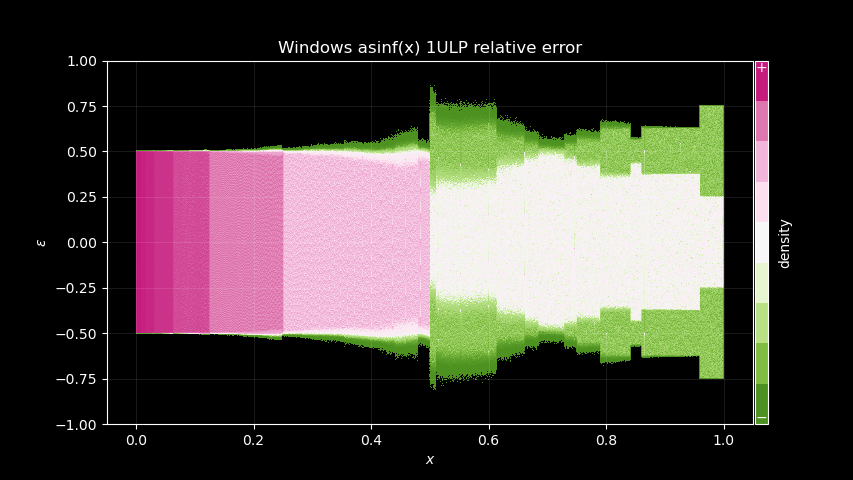
Hmm, that looks nice, what about for instance the GNU glibc implementation?

gnuc_asinf = np.arcsine(x)
gnuc_diff = np.float64(gnuc_asinf) - np.arcsine(np.float64(x))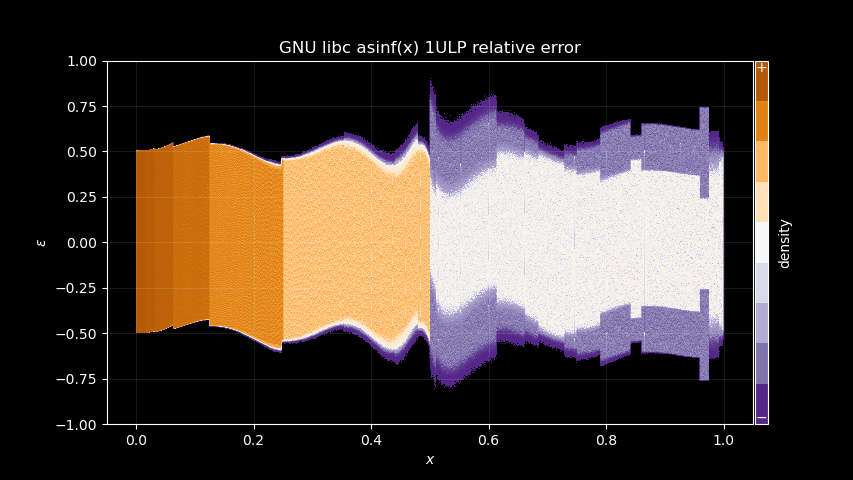

Wow… wobbly!

Does this tell us anything? Well, I think there’s at least a few interesting points to make here:

1. Windows implementation likely uses the same 0.5 domain split as Wine does, as well as the GNU glibc and most other implementations. It is very visible on the pictures, with a clear different error pattern for x > 0.5.

2. The GNU glibc implementation leaks a lot of its polynomial error pattern. Look at our theoretical rational polynomial error above, it’s very similar! Wine and Windows do not show the same, at least nothing obviously visible, so they maybe using higher polynomial degrees, or something different.

3. Wine implementation is really close to Windows in term of signature. More specifically in the right most part of the pictures, GNU glibc shows a segment that does not appear on the other two.

Finding patterns

Let’s try one last thing. Let’s zoom in a bit, close to 0.5, and assume we’re computing something like asin(x) = x + x * P(x²). Can we recognize the error signature of the last + operation?

To find out, we first compute f(x) = asin(x) - x, as if we were infinitely precise (using 64bit floating-point should be enough), then we truncate that back to 32bit and compute the asinf(x) = f(x) + x using 32bit floating point operations.

asin_addx = np.arcsin(np.float64(x)) - np.float64(x)
asin_addx = np.float32(asin_addx) + x

diff = np.float64(asin_addx) - np.arcsin(np.float64(x))

Zooming to the Wine implementation profile for reference, to make some patterns more apparent:

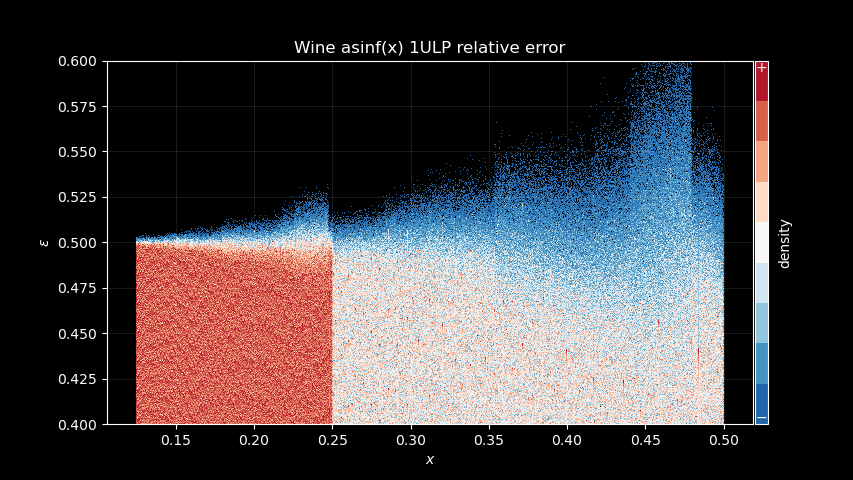
Then the + x operation theoretical induced error:

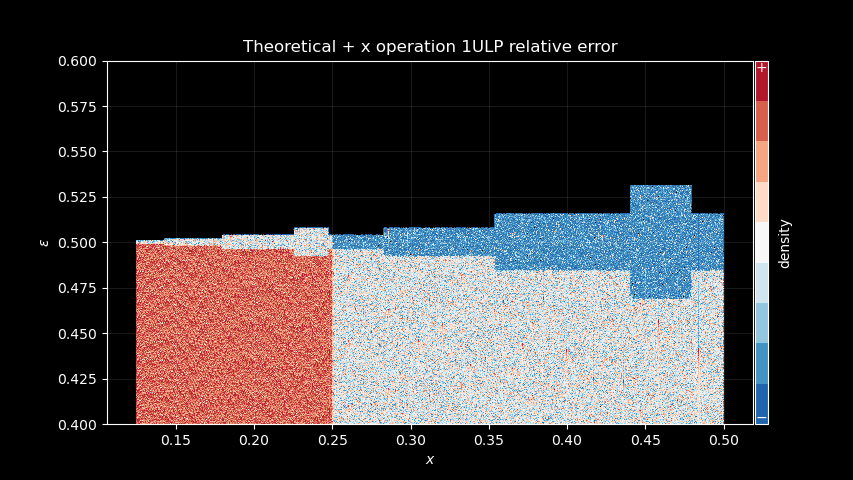
Can you see it?

Okay, let’s go one step further, what about * x + x?

asin_madd = (np.arcsin(np.float64(x)) - np.float64(x)) / np.float64(x)
asin_madd = np.float32(asin_madd) * x + x

diff = np.float64(asin_madd) - np.arcsin(np.float64(x))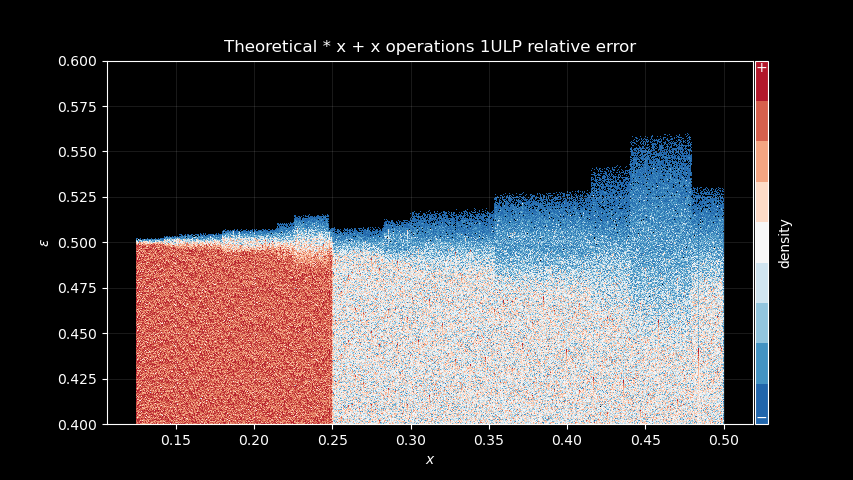

There’s definitely something. And we can compare with Windows signature too, it shows the same kind of patterns:

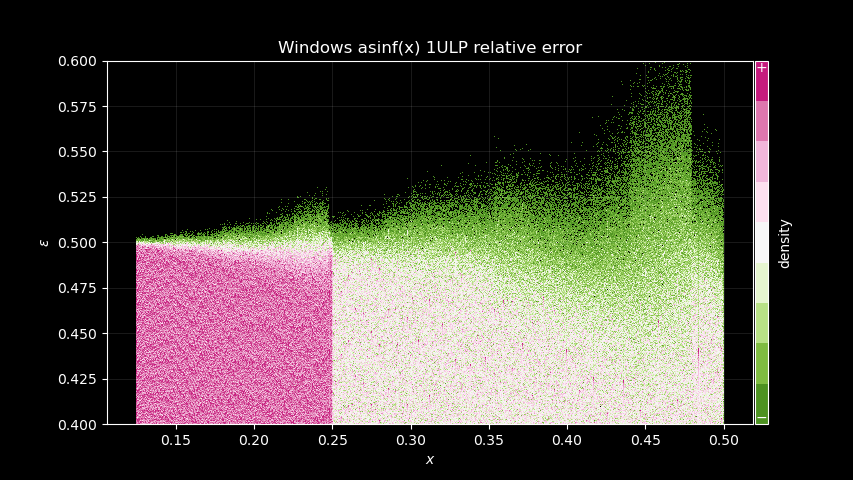
I believe that proves, at least, that the last * x + x operations are done in both implementations, and that Windows uses the same range reduction as described above. Also, because Wine signature is already very similar, I think it is likely that it uses a rational polynomial approximation.

Conclusion

Can we go even further? Can we keep going and reverse engineer the whole thing one operation at a time? Well… I don’t know. The more nested the operations are, the blurrier their error signature gets. At least, doing it visually, like I did here is probably not really going to work.

I believe there’s some information hidden in the errors. There’s actually some more obvious differences between Wine and Windows signature when non-default IEEE 754 rounding modes are used. Can these be exploited to better match the results? Maybe.

At least, even if my analysis didn’t really go anywhere, I still enjoyed the pointless investigation. And we got nice looking pictures too.